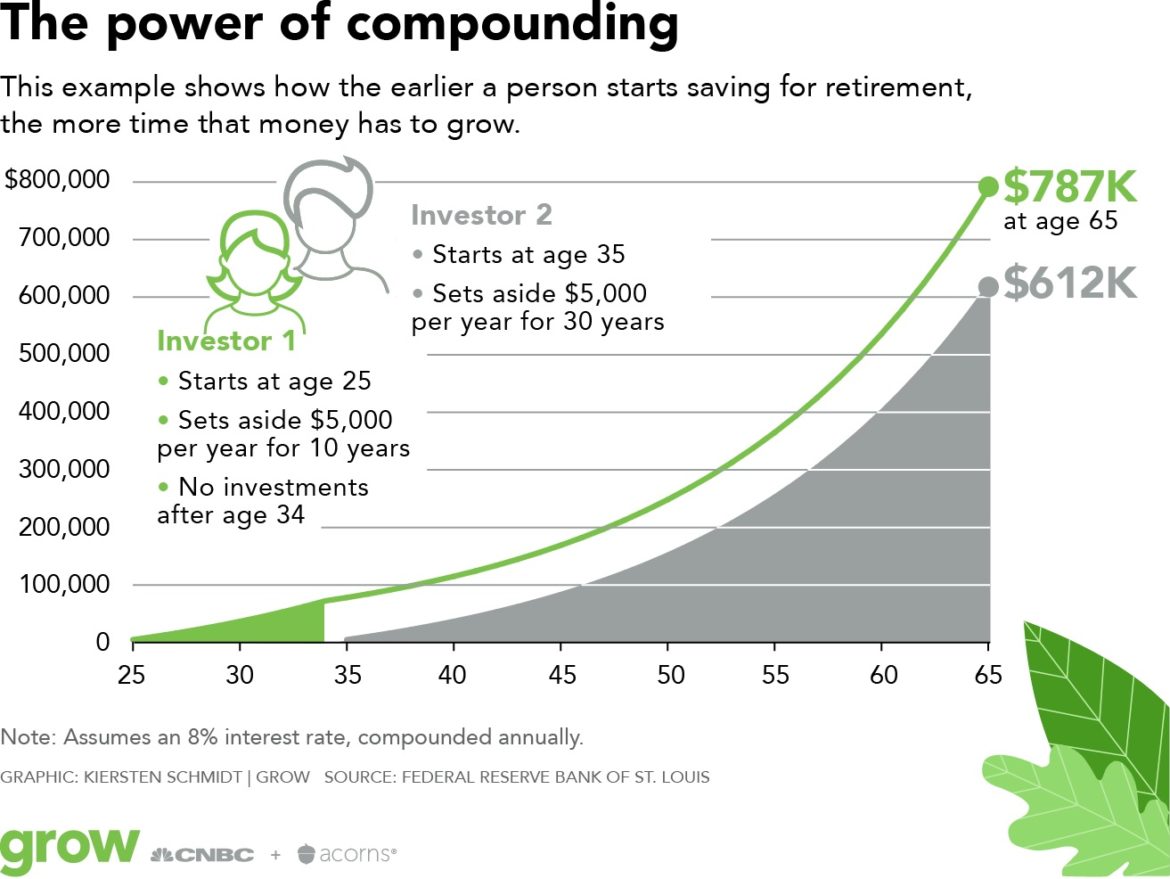
How often do banks compound interest – Wie oft verrechnen Banken Zinsen? Diese Frage ist entscheidend für die Rendite Ihrer Anlagen. Die Häufigkeit der Zinseszinsberechnung, also wie oft die angefallenen Zinsen dem Kapital zugeschlagen werden, beeinflusst maßgeblich das Endergebnis. Von täglich über monatlich bis jährlich variieren die Verzinsungszyklen je nach Bankprodukt und beeinflussen so die letztendlich erzielte Rendite. Wir beleuchten im Folgenden die verschiedenen Zinseszinsperioden und deren Auswirkungen auf Ihr Kapital.
Die mathematische Grundlage der Zinseszinsberechnung ist relativ einfach, doch die praktische Anwendung und die verschiedenen Faktoren, wie Zinssatz, Anlagezeitraum und Gebühren, können die Berechnung komplexer gestalten. Ein tiefes Verständnis dieser Mechanismen ist unerlässlich, um fundierte Anlageentscheidungen zu treffen und das volle Potential des Zinseszins-Effekts zu nutzen.
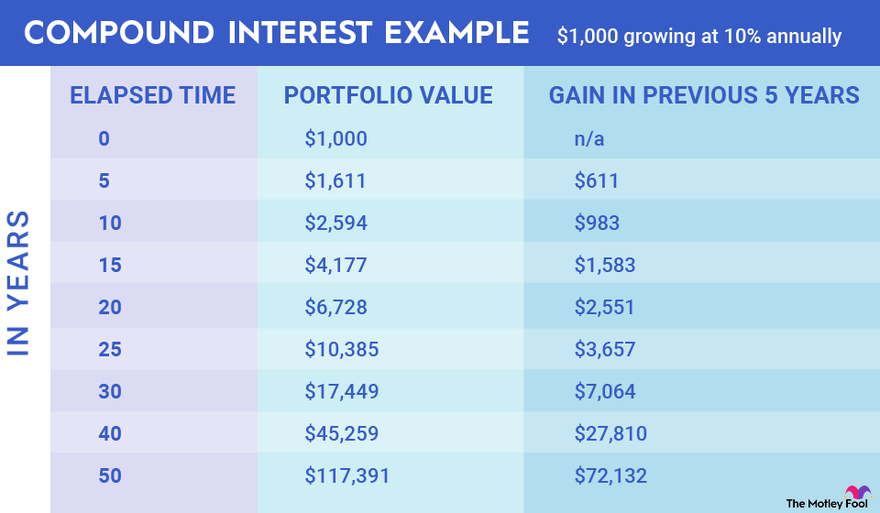
Zinseszinsberechnung
Source: foolcdn.com
Die Zinseszinsberechnung ist ein fundamentales Konzept in der Finanzmathematik und beschreibt, wie sich Zinsen auf bereits angefallene Zinsen addieren und somit einen beschleunigten Vermögensaufbau ermöglichen. Dieses Prinzip ist essenziell für langfristige Investitionen und das Verständnis von verschiedenen Finanzprodukten.
Zinseszinsformel und Einflussfaktoren
Die mathematische Formel zur Berechnung von Zinseszinsen lautet:
Kn = K * (1 + p)n
wobei Kn das Kapital nach n Jahren, K das Anfangskapital, p der Zinssatz (als Dezimalzahl) und n die Anzahl der Jahre darstellt. Die Formel verdeutlicht, wie exponentiell das Kapital im Laufe der Zeit wächst.
Verschiedene Faktoren beeinflussen die Höhe der erzielten Zinseszinsen maßgeblich. Ein höherer Zinssatz (p) führt natürlich zu einem schnelleren Wachstum. Ein längerer Anlagezeitraum (n) verstärkt den Effekt des Zinseszinses exponentiell. Schließlich ist auch das Anfangskapital (K) entscheidend: Ein größeres Anfangskapital generiert höhere Zinsen und somit auch höhere Zinseszinsen.
Grafische Darstellung der Zinseszinsformel, How often do banks compound interest
Stellen Sie sich einen Graphen vor, dessen x-Achse die Zeit (in Jahren) und dessen y-Achse das Kapital darstellt. Die Kurve beginnt bei K und steigt exponentiell an. Die Steigung der Kurve wird durch den Zinssatz (p) bestimmt: Je steiler die Kurve, desto höher der Zinssatz. Die Länge der Kurve entspricht der Anlagezeit (n). Der Endpunkt der Kurve repräsentiert das Kapital nach n Jahren (Kn). Die Krümmung der Kurve verdeutlicht den exponentiellen Wachstumseffekt des Zinseszinses.
Faktoren der Zinseszinsberechnung
| Faktor | Formelzeichen | Beschreibung | Beispiel |
|---|---|---|---|
| Anfangskapital | K | Der Betrag, der zu Beginn angelegt wird. | 10.000 € |
| Zinssatz | p | Der prozentuale Satz, mit dem das Kapital jährlich verzinst wird (als Dezimalzahl). | 0,05 (5%) |
| Laufzeit | n | Die Anzahl der Jahre, für die das Kapital angelegt wird. | 10 Jahre |
| Endkapital | Kn | Das Kapital nach n Jahren, inklusive Zinseszinsen. | 16.289 € (berechnet mit der Formel) |
Zinseszinsperioden bei Banken: How Often Do Banks Compound Interest
Die Häufigkeit der Zinseszinsberechnung ist ein wichtiger Faktor, der die Rendite von Bankprodukten maßgeblich beeinflusst. Je öfter die Zinsen dem Kapital zugeschlagen werden, desto höher fällt der Zinseszins-Effekt aus. Im Folgenden betrachten wir die gängigsten Zinseszinsperioden bei verschiedenen Bankprodukten und deren Auswirkungen auf das Endkapital.
Gängige Zinseszinsperioden bei Bankprodukten
Die Zinseszinsperioden variieren je nach Bankprodukt. Tagesgeldkonten werden in der Regel täglich verzinst, während Festgeldkonten und Sparbücher meist jährlich oder halbjährlich verzinst werden. Manche Banken bieten auch monatliche Verzinsung an. Die konkrete Verzinsungsfrequenz ist immer in den jeweiligen Produktbedingungen der Bank detailliert beschrieben. Eine genaue Prüfung dieser Bedingungen vor Vertragsabschluss ist daher unerlässlich.
Auswirkungen verschiedener Verzinsungsfrequenzen auf das Endkapital
Die unterschiedlichen Verzinsungsfrequenzen führen zu unterschiedlichen Endkapitalbeträgen, selbst bei gleichem Zinssatz. Eine höhere Verzinsungsfrequenz führt zu einem höheren Endkapital, da die Zinsen früher dem Kapital zugeschlagen werden und somit selbst Zinsen erwirtschaften.
| Verzinsungsfrequenz | Beispiel Zinssatz (p.a.) | Endkapital nach 1 Jahr | Endkapital nach 5 Jahren |
|---|---|---|---|
| Jährlich | 3% | 103,00 € (bei 100€ Anlagekapital) | 115,93 € |
| Monatlich | 3% | 103,04 € | 116,15 € |
| Täglich | 3% | 103,05 € | 116,18 € |
*Anmerkung:* Die obigen Berechnungen basieren auf einem fiktiven Anlagekapital von 100€. Die tatsächlichen Endkapitalbeträge hängen vom jeweiligen Anlagebetrag und dem Zinssatz ab.
Darstellung der Zinseszinsberechnung in Kontoauszügen
Die Darstellung der Zinseszinsberechnung in Kontoauszügen variiert von Bank zu Bank. In der Regel werden die gutgeschriebenen Zinsen im Kontoauszug separat ausgewiesen. Manche Banken zeigen detaillierte Aufschlüsselungen der Zinsgutschriften an, andere nur die Summe der gutgeschriebenen Zinsen. Ein genaues Verständnis der Kontoauszüge ist wichtig, um die Zinsentwicklung des eigenen Kontos zu verfolgen und eventuelle Unklarheiten mit der Bank zu klären. Es ist empfehlenswert, sich bei Unklarheiten direkt an die jeweilige Bank zu wenden.
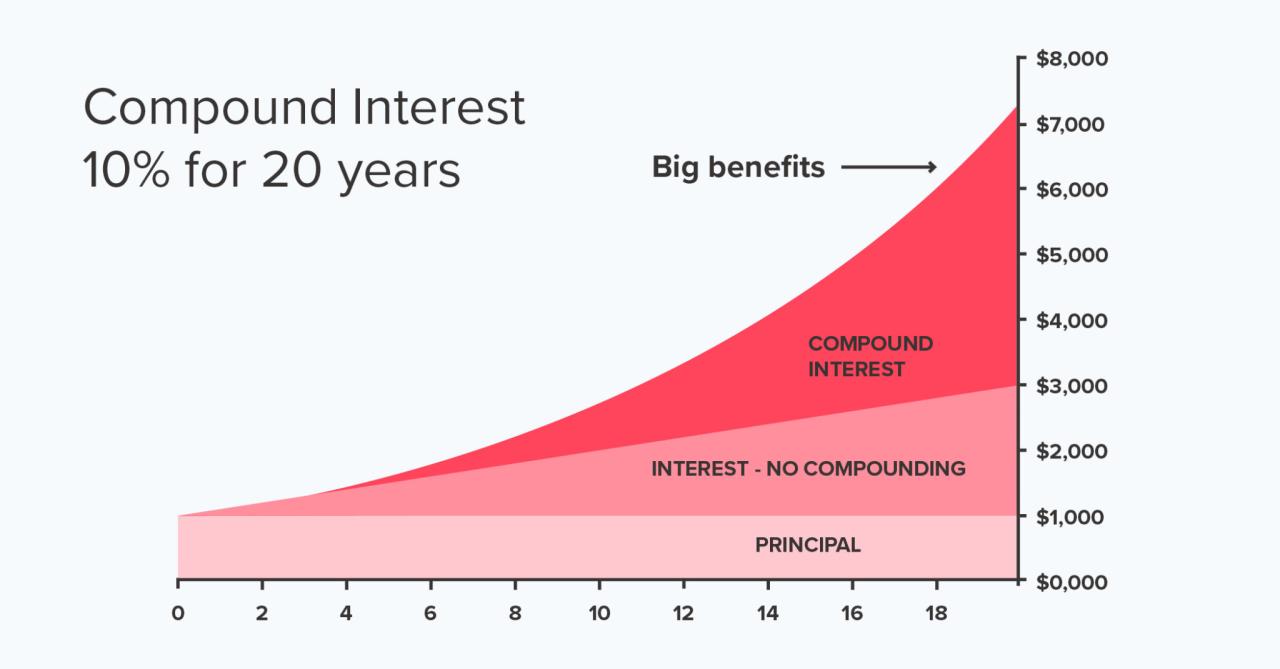
Faktoren, die die Zinseszinsberechnung beeinflussen
Source: swaper.com
Die Berechnung des Zinseszinses, also der Zins auf Zins, ist ein komplexer Prozess, der von verschiedenen Faktoren beeinflusst wird. Ein tieferes Verständnis dieser Faktoren ist essentiell, um die tatsächliche Rendite einer Anlage realistisch einzuschätzen und fundierte Anlageentscheidungen zu treffen. Im Folgenden werden einige der wichtigsten Einflussfaktoren detailliert betrachtet.
Der Einfluss variabler Zinssätze auf die Zinseszinsberechnung
Variable Zinssätze, im Gegensatz zu festen Zinssätzen, unterliegen Schwankungen im Laufe der Zeit. Diese Schwankungen wirken sich direkt auf die Höhe des Zinseszinses aus. Bei steigenden Zinssätzen erhöht sich die Rendite, während fallende Zinssätze zu einer geringeren Rendite führen. Die Prognose zukünftiger Zinssätze ist jedoch schwierig und mit Unsicherheiten behaftet. Eine exakte Zinseszinsberechnung bei variablen Zinssätzen erfordert daher die Berücksichtigung von Zinsprognosemodellen oder die Verwendung von Simulationen, die verschiedene Zinsentwicklungsszenarien durchspielen. Beispielsweise könnte ein Sparkonto mit einem variablen Zinssatz von durchschnittlich 2% über fünf Jahre eine andere Endsumme aufweisen als ein Konto mit einem festen Zinssatz von 2% über den gleichen Zeitraum, da die variablen Zinssätze im Laufe dieser fünf Jahre schwanken könnten.
Auswirkungen von Gebühren und Steuern auf die effektive Rendite
Gebühren und Steuern reduzieren die effektive Rendite einer Anlage, die durch den Zinseszins erzielt wird. Bankgebühren, Depotgebühren oder Verwaltungsgebühren mindern die erzielten Zinsen direkt. Steuern auf Kapitalerträge, wie beispielsweise die Abgeltungsteuer in Deutschland, reduzieren den Nettoertrag. Diese Abzüge wirken sich kumulativ aus, da sie nicht nur auf die anfängliche Anlage, sondern auch auf die im Laufe der Zeit angefallenen Zinsen erhoben werden. Eine realistische Zinseszinsberechnung muss daher immer die anfallenden Gebühren und Steuern berücksichtigen, um die tatsächliche Rendite korrekt zu bestimmen. Nehmen wir beispielsweise an, ein Investment erzielt 5% Zinsen pro Jahr, aber 1% wird durch Gebühren und 20% durch Steuern abgezogen. Die effektive Rendite liegt dann nur noch bei 2,4% (5% – 1% – (5% * 20%) = 2,4%).
Vergleich der Zinseszinsberechnung bei verschiedenen Anlageformen
Die Zinseszinsberechnung variiert je nach Anlageform. Bei Sparbüchern und Festgeldkonten ist der Zinssatz in der Regel festgelegt und die Zinseszinsberechnung relativ einfach. Bei Aktien und Anleihen hingegen schwankt die Rendite stärker, da sie von Kursentwicklungen und Marktrisiken beeinflusst wird. Immobilien bieten ebenfalls Zinseszins-Effekte durch Mieteinnahmen und Wertsteigerungen, jedoch sind diese mit höheren Risiken und längeren Anlagehorizonten verbunden. Der Vergleich der verschiedenen Anlageformen erfordert eine sorgfältige Analyse der jeweiligen Risiken und Renditen, um die optimale Strategie für die individuellen Anlageziele zu finden. Ein direkter Vergleich der Zinseszinsberechnung ist hier aufgrund der unterschiedlichen Risikoprofile und der Komplexität der jeweiligen Renditen nur bedingt möglich. Die Rendite einer Aktie beispielsweise ist nicht vergleichbar mit der Rendite eines Festgeldkontos, da das Risiko deutlich höher ist.
Praktische Beispiele zur Zinseszinsberechnung
Im Folgenden werden anhand konkreter Beispiele die Auswirkungen der Zinseszinsrechnung verdeutlicht. Wir betrachten dabei verschiedene Anlageformen und zeigen die Unterschiede bei unterschiedlichen Verzinsungsperioden auf. Dies soll ein besseres Verständnis für die Wirkungsweise des Zinseszinses ermöglichen.
Festgeldkonto mit jährlicher Verzinsung
Dieses Beispiel veranschaulicht die Zinseszinsrechnung bei einem Festgeldkonto mit einem Anlagebetrag von 10.000 Euro, einem jährlichen Zinssatz von 3% über einen Zeitraum von 10 Jahren. Die Verzinsung erfolgt jährlich. Die Berechnung erfolgt nach folgender Formel: Endkapital = Anfangskapital * (1 + Zinssatz)^Laufzeit.
| Jahr | Anfangskapital | Zinsen | Endkapital |
|---|---|---|---|
| 1 | 10000,00 € | 300,00 € | 10300,00 € |
| 2 | 10300,00 € | 309,00 € | 10609,00 € |
| 3 | 10609,00 € | 318,27 € | 10927,27 € |
| 4 | 10927,27 € | 327,82 € | 11255,09 € |
| 5 | 11255,09 € | 337,65 € | 11592,74 € |
| 6 | 11592,74 € | 347,78 € | 11940,52 € |
| 7 | 11940,52 € | 358,22 € | 12298,74 € |
| 8 | 12298,74 € | 368,96 € | 12667,70 € |
| 9 | 12667,70 € | 380,03 € | 13047,73 € |
| 10 | 13047,73 € | 391,43 € | 13439,16 € |
Sparkonto mit monatlicher Verzinsung
Im Gegensatz zum vorherigen Beispiel wird hier ein Sparkonto mit monatlicher Verzinsung betrachtet. Bei gleichem Anlagebetrag (10.000 Euro) und gleichem jährlichen Zinssatz (3%), jedoch mit monatlicher Zinsgutschrift, ergibt sich ein höherer Endbetrag aufgrund der häufigeren Zinseszinsberechnung. Der monatliche Zinssatz berechnet sich als 3%/12 = 0,25%. Die Formel zur Berechnung des Endkapitals bei monatlicher Verzinsung lautet: Endkapital = Anfangskapital * (1 + monatlicher Zinssatz)^(Laufzeit in Monaten). Der Unterschied zum jährlichen Beispiel liegt in der höheren Anzahl der Zinsperioden, was zu einer stärkeren Wirkung des Zinseszinses führt. Die detaillierte Berechnung würde eine umfangreiche Tabelle erfordern und ist hier aus Platzgründen nicht vollständig dargestellt. Jedoch ist ersichtlich, dass das Endkapital nach 10 Jahren bei monatlicher Verzinsung höher ausfallen wird als bei jährlicher Verzinsung.
Kredit mit Zinseszinsberechnung
Die Zinseszinsrechnung wirkt sich auch bei Krediten aus. Hier werden die Zinsen auf den noch offenen Kreditbetrag berechnet, was zu einer höheren Gesamtbelastung führt. Nehmen wir beispielsweise einen Kredit über 20.000 Euro mit einem jährlichen Zinssatz von 5% und einer Laufzeit von 5 Jahren bei jährlicher Tilgung. Die Zinsen werden jedes Jahr auf den noch offenen Kreditbetrag berechnet und mit diesem zusammen zur Tilgung addiert. Die genaue Berechnung der einzelnen Tilgungsraten und Zinsaufwendungen erfordert eine komplexere Formel und wird hier aus Platzgründen nicht vollständig dargestellt. Es ist jedoch wichtig zu verstehen, dass die Zinseszinsrechnung auch bei Krediten eine erhebliche Rolle spielt und zu höheren Gesamtkosten führt.
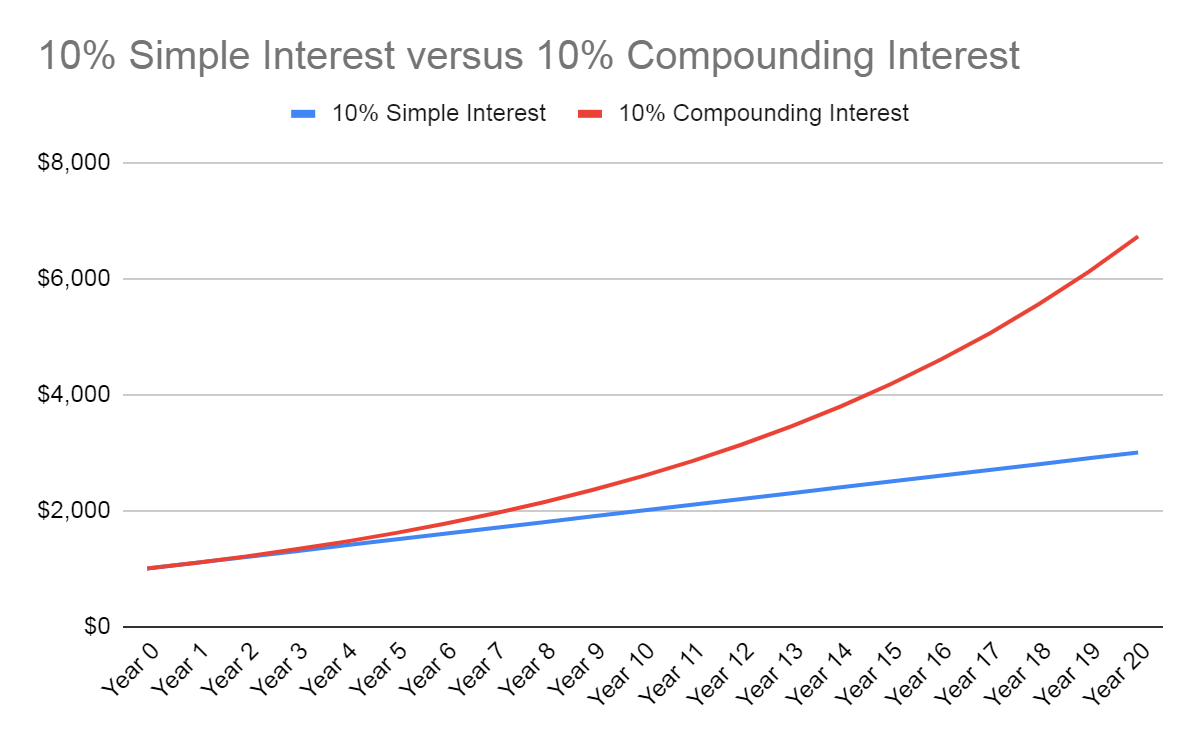
Effektiver Jahreszins vs. Nominalzins
Source: financestrategists.com
Der Nominalzins und der effektive Jahreszins sind zwei wichtige Kennzahlen, die die Kosten eines Kredits oder die Rendite einer Anlage beschreiben. Sie unterscheiden sich jedoch deutlich in ihrer Aussagekraft, da der Nominalzins vereinfacht die Zinsen angibt, während der effektive Jahreszins die tatsächlichen Kosten oder Erträge widerspiegelt. Ein umfassendes Verständnis beider Zinsarten ist essentiell für fundierte Finanzentscheidungen.
Der Nominalzins gibt den vereinbarten Zinssatz pro Jahr an. Er berücksichtigt jedoch nicht die Auswirkungen der Zinseszinsrechnung bei mehrmaliger Zinsgutschrift im Jahr. Der effektive Jahreszins hingegen berechnet die tatsächliche Verzinsung unter Berücksichtigung der Zinseszinswirkung und aller anfallenden Gebühren. Er stellt somit den realen Zinssatz dar, der über einen Zeitraum von einem Jahr erzielt wird.
Berechnung des effektiven Jahreszinses
Zur Berechnung des effektiven Jahreszinses werden verschiedene Informationen benötigt. Diese beinhalten den Nominalzins, die Anzahl der Zinsperioden pro Jahr (z.B. monatlich, vierteljährlich) und alle anfallenden Kosten wie beispielsweise Bearbeitungsgebühren oder Kontoführungsgebühren. Die Formel zur Berechnung des effektiven Jahreszinses ist komplex und wird üblicherweise mithilfe von Finanzrechnern oder Software ermittelt. Ein vereinfachtes Beispiel wäre die Formel für jährliche Verzinsung: Effektiver Jahreszins = (1 + Nominalzins/Anzahl der Zinsperioden)^Anzahl der Zinsperioden – 1. Für komplexere Szenarien mit zusätzlichen Kosten ist eine detailliertere Berechnung notwendig.
Bedeutung des effektiven Jahreszinses für den Anleger
Der effektive Jahreszins ist für Anleger von entscheidender Bedeutung, da er einen direkten Vergleich verschiedener Anlagemöglichkeiten ermöglicht. Im Gegensatz zum Nominalzins zeigt er die tatsächliche Rendite an, die unter Berücksichtigung aller Faktoren erzielt wird. Ein höherer effektiver Jahreszins signalisiert eine höhere Rendite. So kann ein Anleger beispielsweise zwei Anlageprodukte mit unterschiedlichen Nominalzinsen und Zinszahlungsfrequenzen vergleichen und anhand des effektiven Jahreszinses die rentablere Option auswählen. Dies ist besonders wichtig bei der Auswahl von Sparprodukten oder Krediten, um die tatsächlichen Kosten oder Erträge realistisch einzuschätzen. Ein Beispiel: Ein Sparkonto mit einem Nominalzins von 4% und jährlicher Zinszahlung hat einen effektiven Jahreszins von 4%. Ein anderes Konto mit einem Nominalzins von 3,9% und monatlicher Zinszahlung kann jedoch einen höheren effektiven Jahreszins aufweisen, da die Zinseszinswirkung die Rendite steigert.
Zusammenfassend lässt sich sagen, dass die Häufigkeit der Zinseszinsberechnung einen erheblichen Einfluss auf die langfristige Entwicklung Ihres Kapitals hat. Eine tägliche oder monatliche Verzinsung führt im Vergleich zur jährlichen Verzinsung zu einem höheren Endkapital. Es ist daher ratsam, bei der Auswahl von Bankprodukten nicht nur den Nominalzins, sondern auch die Verzinsungsfrequenz und den effektiven Jahreszins zu berücksichtigen. Ein sorgfältiger Vergleich verschiedener Angebote ermöglicht es Ihnen, die optimale Anlage für Ihre individuellen Bedürfnisse zu finden und den Zinseszins-Effekt optimal zu nutzen.